This seminar aims to present recent progress around modern analysis. The topics will cover the current trend of functional analysis, harmonic analysis and related fields in a large sense, for example operator algebras, Banach space and operator space theory, modern and noncommutative harmonic analysis, quantum probability, quantum information, topological quantum groups and so on.
The seminar is held on Wednesdays in a hybrid form; online access will be provided for speakers and audiences who cannot come to Harbin in person.
Please follow this link to subscribe to our mailing list and receive the information if you are interested.
Contact: Xudong LAI (xudonglai AT hit.edu.cn), Simeng WANG (simeng.wang AT hit.edu.cn)
Upcoming talks
December 17, 2025. 16:00 (Beijing time)
Speaker: Gan Yao
Title: Optimal Hypercontractivity and Log-Sobolev inequalities on Cyclic Groups Z_{m·2k}
Abstract
For 1≤p≤q<∞ and n in {3·2k, 2k} with k≥1, we prove that the Poisson-like semigroup Pt on Zn, associated with the word length ψn(k)=min(k,n-k), is hypercontractive from Lp![]() to Lq if and only if t≥(1/2)log((q-1)/(p-1)). We establish sharp Log-Sobolev inequalities with the optimal constant 2, by performing a KKT analysis, and lifting from the base cases Z6 and Z4 via a Cooley-Tukey n to 2n comparison of Dirichlet forms. The general case for arbitrary n remains open.
to Lq if and only if t≥(1/2)log((q-1)/(p-1)). We establish sharp Log-Sobolev inequalities with the optimal constant 2, by performing a KKT analysis, and lifting from the base cases Z6 and Z4 via a Cooley-Tukey n to 2n comparison of Dirichlet forms. The general case for arbitrary n remains open.
Past talks
(Playlist of recordings: https://space.bilibili.com/1171904096/channel/collectiondetail?sid=668900)
October 22, 2025. 16:00 (Beijing time)
Speaker: Fedor Sukochev
Title: Optimal distribution estimates for commutators and Marcinkiewicz multipliers
Abstract
The main objective of this talk is to discuss the distributional estimates for (i) commutators with Calderón-Zygmund integral operators; (ii) Marcinkiewicz multipliers; (iii) Littlewood-Paley square function, via semigroup { 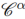 }α>0 generated by Cesàro operator. In each of the cases (i)-(iii) we obtain new estimates of the distribution of elements in the range of the underlying operators in terms of the distribution function of the input function. Our method allows us to obtain optimal estimates shedding additional light at the results due to Pérez (1995), Tao and Wright/Bakas et al. (2001/2024), Bourgain (1989). The main feature of the distributional form inequalities lies in its broad applicability across diverse problems in analysis, e.g. they allow obtaining estimates in wide range of symmetric quasi-Banach interpolation spaces between Lp and Lq(1 < p < q < ∞), not just for Lp-spaces (1 < p < ∞). This is a joint work with Fulin Yang, Dmitriy Zanin and Dejian Zhou accepted for publication in Math. Annalen.
}α>0 generated by Cesàro operator. In each of the cases (i)-(iii) we obtain new estimates of the distribution of elements in the range of the underlying operators in terms of the distribution function of the input function. Our method allows us to obtain optimal estimates shedding additional light at the results due to Pérez (1995), Tao and Wright/Bakas et al. (2001/2024), Bourgain (1989). The main feature of the distributional form inequalities lies in its broad applicability across diverse problems in analysis, e.g. they allow obtaining estimates in wide range of symmetric quasi-Banach interpolation spaces between Lp and Lq(1 < p < q < ∞), not just for Lp-spaces (1 < p < ∞). This is a joint work with Fulin Yang, Dmitriy Zanin and Dejian Zhou accepted for publication in Math. Annalen.
October 15, 2025. 16:00 (Beijing time)
Speaker: Javier Parcet(Instituto de Ciencias Matemáticas)
Title: Riesz-Schur transforms
Abstract
Fourier multipliers are closely related to Schur multipliers with Toeplitz symbols. Classical results from Fourier analysis are recently finding extensions in the more general setting of nonToeplitz Schur multipliers. In this talk, I will report on recent results about nonToeplitz Riesz transforms. This refines Grothendieck-Haagerup’s endpoint criterion with a new condition for the Schatten p-boundedness of Schur multipliers and strengthens Potapov/Sukochev’s solution of Arazy’s conjecture. Our approach is much simpler than previous harmonic analysis and probabilistic ones. As an application, we find a very simple proof of recent criteria for Schur multipliers of Hörmander-Mikhlin and Marcinkiewicz type. Joint work with A. González-Pérez, J. Pérez-García and É. Ricard.
May 28, 2025. 14:30 (Beijing time)
Speaker: Raphaël Ponge (Sichuan University)
Title: Noncommutative Geometry and Semiclassical Analysis on Quantum Tori
Abstract
The semiclassical Weyl’s law is a landmark result in semiclassical analysis. In this lecture I will explain how it ultimately holds for a large class of quantum spaces. We will use this framework to solve a conjecture of E. McDonald and myself on semiclassical Weyl’s laws for curved quantum tori, i.e., quantum tori equipped with arbitrary Riemannian metrics. On the way we will see how to get spectral asymptotics for all negative order pseudodifferential operators on noncommutative tori. As a further application, we shall recover recent results of Sukochev-Xiong-Zanin on asymptotics for singular values of quantized derivatives on (flat) noncommutative tori. This bypasses the use of the $C^*$-algebra approach to the principal symbol used in the original article of Sukochev-Xiong-Zanin.
May 28, 2025. 16:00 (Beijing time)
Speaker: Tattwamasi Amrutam (IMPAN)
Title: Invariant Subalgebras of the reduced group C*-algebras
Abstract
Let be a countable discrete group. Associated with it is the reduced group-algebra and the group von Neumann algebra. It is interesting to ask which group properties are reflected at the group von Neumann algebra or reduced group-algebra level. We say that has-invariant subalgebra rigidity property (-ISR property) if every invariant-subalgebra is of the form for some normal subgroup.
May 21, 2025. 9:00 (Beijing time)
Speaker: Sayan Das (East China Normal University)
Title: Poisson boundaries of groups and von Neumann algebras
Abstract
Furstenberg introduced the notion of Poisson boundary of groups in 1960s. Since then, Poisson boundaries have played a pivotal role in ergodic theory, and measured group theory to study various rigidity phenomenon associated with groups and their actions.
Motivated by this, Alain Connes proposed that a corresponding notion of Poisson boundaries for von Neumann algebras needs to be developed in order to study rigidity aspects of von Neumann algebras. In this talk, I will explain the notion of classical Poisson boundaries, and their noncommutative counterpart, which was developed by Prof. Jesse Peterson and the speaker. I will also mention a few applications.
May 21, 2025. 10:30 (Beijing time)
Speaker: Prayagdeep Parija (Virginia Tech)
Title: Random quotients of hyperbolic groups and Property (T)
Abstract
What does a typical quotient of a group look like? Gromov looked at the density model of quotients of free groups. The density parameter d measures the rate of exponential growth of the number of relators compared to the size of the Cayley ball. Using this model, he proved that for d < 1/2, the typical quotient of a free group is non-elementary hyperbolic. Ollivier extended Gromov’s result to show that for d < 1/2, the typical quotient of many hyperbolic groups is also non-elementary hyperbolic.Zuk and Kotowski–Kotowski proved that for d > 1/3, a typical quotient of a free group has Property (T). We show that (in a closely related density model) for 1/3 < d < 1/2, the typical quotient of a large class of hyperbolic groups is non-elementary hyperbolic and has Property (T). This provides an answer to a question of Gromov (and Ollivier).
May 16, 2025. 10:00 (Beijing time)
Speaker: Cheng Zhang (Tsinghua University)
Title: Strichartz estimates for orthonormal systems on compact manifolds
Abstract
We establish new Strichartz estimates for orthonormal systems on compact Riemannian manifolds in the case of wave, Klein-Gordon and fractional Schrödinger equations. Our results generalize the classical (single-function) Strichartz estimates on compact manifolds by Kapitanski, Burq-Gérard-Tzvetkov, Dinh, and extend the Euclidean orthonormal version by Frank-Lewin-Lieb-Seiringer, Frank-Sabin, Bez-Lee-Nakamura. On the flat torus, our new results for the Schrödinger equation cover prior work of Nakamura, which exploits the dispersive estimate of Kenig-Ponce-Vega. We achieve sharp results on compact manifolds by combining the frequency localized dispersive estimates for small time intervals with the duality principle due to Frank-Sabin. We construct examples to show these results can be saturated on the sphere, and we can improve them on the flat torus by establishing new decoupling inequalities for certain non-smooth hypersurfaces. As an application, we obtain the well-posedness of infinite systems of dispersive equations with Hartree-type nonlinearity. This is joint work with Xing Wang (Hunan Univ.) and An Zhang (Beihang Univ.).
April 23, 2025. 10:00 (Beijing time)
Speaker: Georgios Katsimapas (Harbin Engineering University)
Title: Free probability theory, notions of entropy and applications
Abstract
The theory of free probability was developed by Voiculescu in the 1980’s as an extension of classicalprobability to the non-commutative setting and aims to study algebras of operators on Hilbertspaces from a probabilistic point of view. The connection of free probability with random matrixtheory, as well as the development of notions of entropy in the non-commutative framework, lead tosignificant breakthroughs regarding the structure of certain von Neumann algebras. More recently,in 2013 Voiculescu laid the foundations of bi-free probability theory, which extends the free settingand involves the simultaneous study of left and right actions of algebras on reduced free productspaces. In this talk, we will give an overview of the contributions of free probability theory to thefield of operator algebras and will discuss the development of notions of entropy within the contextof bi-free probability theory.
April 8, 2025. 16:00 (Beijing time)
Speaker: Chunguang Li (Northeast Normal University)
Title: Remarks on Villadsen algebras
Abstract
Villadsen algebras of the first type were constructed in 1998 as examples of simple unital C∗-algebras which have perforation in their ordered K0 group. This class of C∗-algebras lies outsidethe scope of the current classification theorem, as Villadsen algebras do not absorb the Jiang-Su algebra Z tensorially. We shall show that such algebras can be classified by the K0 group together with the radius of comparison. Also, we shall show that such algebras are singly generated. These works are joint with Elliott, Niu and Ruzicka.
April 8, 2025. 14:30 (Beijing time)
Speaker: Qingnan An (Northeast Normal University)
Title: On the classification of 1-ASH algebras of real rank zero
Abstract
Wewill discuss some recent progress on the classification for C∗-algebras of real rank zero. Examples will be given to show the following: (1) There exists a real rank zero inductive limit of 1-NCCW complexes which is not an AD algebra, when K1 is torsion-free or has bounded torsion; (2) Total K-theory is not a complete invariant for 1-ASH algebras of real rank zero. This series of works are jointed with Søren Eilers, Guihua Gong and Zhichao Liu.
March 19, 2025. 14:30 (Beijing time)
Speaker: Jorge Pérez García (ICMAT)
Title: Riesz transforms as Schur multipliers
Abstract
Schur multipliers can be understood as a flexible generalization of Fourier multipliers, making it natural to explore how classical theorems in the Fourier case extend to this setting. In this talk, we will introduce a result concerning the Schur analogue of Riesz transforms, with applications ranging from new criteria for the Sp-boundedness of Schur multipliers to simplified proofs of some well-known results. This is joint work with Adrián González-Pérez, Javier Parcet, and Éric Ricard.
December 11, 2024. 14:30 (Beijing time)
Speaker: Hua Wang (IMPAN)
Title: Some aspects of a theory of locally convex Hopf algebras
Abstract
We will give an overview of a recent theory of locally convex Hopf algebras, with an emphasis on the duality aspect. After motivating and introducing the theoretical framework, we will describe how Hopf algebras, compact and discrete quantum groups, locally compact groups, Lie groups, as well as their respective duals, can all give rise to examples in various ways. Then the emphasis shifts to the non-locally compact aspects of theory. The main result is that under the very weak assumption that the topology of a topological group $G$ is compactly generated, one can fully describe $G$ using only the locally convex Hopf algebra of continuous functions on it. This goes much beyond the previously well-known locally compact case, and includes interesting examples such as all metrizable groups, all topological groups that admit a cellular decomposition, etc. On the non-commutative side, we will describe some new interesting topological quantum groups that arise naturally but seem to go beyond the current Kustermans-Vaes framework. Time permitting, exploiting some deep structural resuts related to Hilbert's fifth problem, we shall mention how one can describe a second countable locally compact group using a variant of Bruhat's notion of regular (smooth) functions on it.
November 27, 2024. 14:30 (Beijing time)
Speaker: Ting Lu (Harbin Institute of Technology)
Title: The Haar state of O(SLq(3)) on a monomial basis
Abstract
The quantum group \mathcal{O}(SL_q(n)) is a non-(co)commutative Hopf algebra dual to the Jimbo-Drinfeld quantum group $\mathcal{U}_q(sl(n))$. It is known that O(SLq(3)) becomes a pre-Hilbert space with the Haar state as the inner product. The matrix coefficients of the Peter-Weyl decomposition of \mathcal{O}(SL_q(n)) are orthogonal with respect to the inner product. However, there is no orthonormal basis on this pre-Hilbert space due to a lack of efficient methods to evaluate the Haar state values of monomials on $\mathcal{O}(SL_q(n)). In this talk, we investigate the Haar state on \mathcal{O}(SL_q(3)). We will define a monomial basis that spans the linear subspace consisting of elements with non-zero Haar state values. Then, we give the Haar state values of those monomials in the basis as rational polynomials in variable q. We will also discuss the method to achieve an orthonormal basis which is proposed by Noumi, Yamada, and Mimachi.
November 20, 2024. 14:30 (Beijing time)
Speaker: Heon Lee (Harbin Institute of Technology)
Title:First-order differential calculi and Laplacians on q-deformations of compact semisimple Lie groups
Abstract
November 13, 2024. 16:00 (Beijing time)
Speaker: Anar Dosi (Harbin Engineering University)
Title: Noncommutative formal geometry of a contractive quantum plane
Abstract,video,slides
The present talk is devoted to the noncommutative complex analytic geometry of a contractive quantum plane from the formal completion point of view. The formal completion of an Arens-Michael envelope of the quantum plane possesses the same spectrum to be the union of two copies of the complex plane. It turns out that it can be extended up to an Arens-Michael-Fréchet algebra sheaf, which results in the noncommutative analytic space, whose base topological space is the same spectrum. Moreover, that sheaf can be obtained as the deformation quantization of the related commutative analytic space. As the basic tool we use the fibered products of the Fréchet sheaves. To find out a key link between the transversality relation of the noncommutative sections versus to a left Fréchet module we discuss the related topological homology problems, and the related noncommutative Taylor spectrum of the module.
October 16, 2024. 14:30 (Beijing time)
Speaker: Zhizheng Yu (Harbin Institute of Technology)
Title: Szlenk and -dentability indices of C*-algebras
Abstract, video
Let be an infinite dimensional C*-algebra and. We compute the Szlenk index of and, and show that and, where is the noncommutative Cantor-Bendixson index, is the minimum ordinal number which is greater than of the form for some and we agree that and. As an application, we compute the Szlenk index [respectively,-dentability index] of a C*-tensor product of non-zero C*-algebras and in terms of and [respectively, and]. When is a separable C*-algebra, we show that there exists such that and, where is the C*-subalgebra of generated by.
October 9, 2024. 14:30 (Beijing time)
Speaker: Kai Zeng (Ghent University)
Title: Schatten properties of commutators on twisted crossed products
Abstract, slides, video
In this talk, we study Fourier multiplier commutators on a twisted crossed product . We will characterise their Schatten -class membership by that of their symbols in the associated Besov space. In addition, we show a formula on the Dixmier trace, which also gives us a characterization of the weak Schatten -class membership of these commutators by a Sobolev space. As an example, our results applied to noncommutative Euclidean Space.
June 5, 2024. 14:30 (Beijing time)
Speaker: Yonglong Li (Xi'an Jiaotong University)
Title: Renyi Entropy Rate of Stationary Ergodic Processes
Abstract, video
Renyi entropy plays an important role in information theory and large deviation theory. For stochastic processes with good properties as mixing, Renyi entropy rate converges to the Shannon entropy rate. However, in this talk we will give an example to show that for general stationary and ergodic processes, the continuity of Renyi entropy rate breaks down at α=1. This is a joint work with Chengyu Wu, Li Xu and Guangyue Han.
June 5, 2024. 16:00 (Beijing time)
Speaker: Lei Yu (Nankai University)
Title: Hypercontractive inequalities and their extensions
Abstract, video
Hypercontractive inequalities are a class of functional inequalities that strengthen the well-known Holder inequalities. These inequalities have found many applications in functional analysis, probability theory, discrete Fourier analysis, theoretical computer science, etc., especially in dealing with extremal problems in the geometry of high-dimensional spaces. In this talk, we will introduce hypercontractive inequalities and their extensions, including the information-theoretic characterization of hypercontractive inequalities, a non-linear strengthening of hypercontractive inequalities, and the opposite version of hypercontractive inequalities, called anti-contractive inequalities.
May 22, 2024. 14:30 (Beijing time)
Speaker: Raphaël Ponge (Sichuan University)
Title: Noncommutative Geometry, Semiclassical Analysis, and Weak Schatten p-Classes
Abstract
The first part of the lecture will survey the main facts regarding Connes’ integration, Weyl’s laws for compact operators and their relationships with semiclassical analysis. In particular, we will explain the link between Connes’ integration formula and semiclassical Weyl’s laws. This will include some background on Schatten $p$-classes and the Birman-Schwinger principle. The 2nd part will present new results regarding semiclassical Weyl’s laws and integration formulas for noncommutative manifolds (i.e., spectral triples). This improves and simplifies recent results of McDonald-Sukochev-Zanin and Kordyukov-Sukochev-Zanin. For the Dirichlet and Neumann problems on Euclidean domains and closed Riemannian manifolds this enables us to recover the semiclassical Weyl’s laws in those settings from old results of Minakshisundaram and Pleijel from the late 40s. For closed manifolds this also allows us to recover the celebrated Weyl’s laws of Birman-Solomyak for negative-order pseudodifferential operators. A further set of examples is provided by Schrödinger operators associated to sub-Laplacians on sub-Riemannian manifolds, including contact manifolds and Baouendi-Grushin example. Finally, we will explain how this framework enables us to get semiclassical Weyl’s laws for noncommutative tori. This will solve conjectures by Edward McDonald and the speaker.
May 8, 2024. 14:30 (Beijing time)
Speaker: Dmitriy Zanin (University of New South Wales)
Title: Commutators in Harmonic Analysis: optimal estimates and asymptotic behavior
April 17, 2024. 14:30 (Beijing time)
Speaker: Heon Lee (Seoul National University)
Title: Analytic subalgebras of weighted Fourier algebras and complexification of Lie groups
Abstract, slides
In this talk, we focus on how we can interpret the actions of the elements in the Gelfand spectrum of a weighted Fourier algebra on connected Lie groups. They can be viewed as evaluations on specific points of the complexification of the underlying Lie group. For this purpose, we need to introduce a particular dense subalgebra of the weighted Fourier algebra, which we call an analytic subalgebra. We first introduce an analytic subalgebra allowing a “local” solution for general connected Lie groups. We will demonstrate that a “global” solution is also possible for simply connected nilpotent Lie groups.
April 17, 2024. 16:00 (Beijing time)
Speaker: Hongyin Zhao (University of New South Wales)
Title: Kuroda’s theorem for n-tuples in semifinite von Neumann algebras
Abstract, slides, video
Kuroda’s Theorem is one of the fundamental results in perturbation theory. It states that, if J is a Banach ideal in 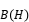 that is not contained in the trace class, then for every self-adjoint operator b on H and every
that is not contained in the trace class, then for every self-adjoint operator b on H and every 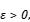 there exists a diagonal operator d on H such that ∥b − d∥J < ε. In this talk, we will talk about an extension of Kuroda’s theorem for n-tuples of commuting self-adjoint operators affiliated with a semifinite von Neumann algebra
there exists a diagonal operator d on H such that ∥b − d∥J < ε. In this talk, we will talk about an extension of Kuroda’s theorem for n-tuples of commuting self-adjoint operators affiliated with a semifinite von Neumann algebra 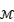 , with respect to symmetric spaces associated with
, with respect to symmetric spaces associated with 
April 10, 2024. 14:30 (Beijing time)
Speaker: Hong-Wei Zhang (Paderborn University)
Title: L2-spectrum, convergence exponents, and temperdness on locally symmetric spaces
Abstract, slides, video
In this talk we will discuss, on a locally symmetric space of higher rank and infinite volume, the relations between objects in three different topics: the bottom of the L2-spectrum of the Laplace-Beltrami operator, the convergence rate of the discrete subgroup, and the tempered representations.
April 3, 2024. 14:30 (Beijing time)
Speaker: Runlian Xia (University of Glasgow)
Title: Fourier multipliers on HNN extensions
Abstract, slides, video
Amalgamated free products and HNN extensions are the two fundamental objects in the Bass-Serre theory. In this talk, we will introduce some Lp-bounded (1 <p < ∞) Fourier multipliers for HNN extensions, with the help of Khinchine type inequalities on these groups. This work is a continuation of a recent work with Adrián González and Javier Parcet. It is related to the results of Mei, Ricard and Xu who proved Lp-boundedness of the same type of Fourier multipliers on amalgamated free products of von Neumann algebras.
March 27, 2024. 14:30 (Beijing time)
Speaker: Marat Pliev (Southern Mathematical Institute of Russian Academy of Science)
Title: Compact orthogonally additive operators on Banach lattices
Abstract, slides, video
In this talk we present the state of the art of the theory of compact orthogonally additive (in general nonlinear) operators in Banach lattices.
In particular, the nonlinear version of the famous Dodds-Fremlin theorem is discussed.
March 27, 2024. 16:00 (Beijing time)
Speaker: Zheng Li (Politecnico di Milano)
Title: Exponential Ergodicity in Certain Quantum Markov Semigroups
Abstract, slides, video
Speaker: Xuerui Yang (University of Illinois Urbana-Champaign)
Title:An improvement on Gauss's Circle Problem and Dirichlet's Divisor Problem
Abstract, slides, video
Using Bombieri-Iwaniec method, we establish an improvement on both Gauss's Circle Problem and Dirichlet's Divisor Problem. More precisely, we derive a new estimate for the first spacing problem and combine it with Huxley's results on the second spacing problem. In this talk, I will talk about several methods to deal with exponential sums on the integer ring, with focus on the Bombieri-Iwaniec method. After that, I will talk about several results in decoupling theory as well as some rough ideas in the proofs.
December 13, 2023. 14:30 (Beijing time)
Speaker: Ranyiliu Chen (University of Copenhagen)
Title:Resource-dependent complexity of quantum channels
Abstract, slides, video
Self-testing allows a classical verifier to infer a quantum mechanical description of untrusted quantum devices that she interacts with in a black-box manner. Somewhat contrary to the black-box paradigm, existing self-testing results tend to presuppose conditions that constrain the operation of the untrusted devices. A common assumption is that these devices perform a projective measurement of a pure quantum state. Naturally, in the absence of any prior knowledge it would be appropriate to model these devices as measuring a mixed state using POVM measurements, since the purifying/dilating spaces could be held by the environment or an adversary.
We prove a general theorem allowing to remove these assumptions, thereby promoting most existing self-testing results to their assumption-free variants. On the other hand, we pin-point situations where assumptions cannot be lifted without loss of generality. As a key (counter)example we identify a quantum correlation which is a self-test only if certain assumptions are made. Remarkably, this is also the first example of a correlation that cannot be implemented using projective measurements on a bipartite state of full Schmidt rank.
November 15, 2023. 14:30 (Beijing time)
Speaker: Peixue Wu (University of Waterloo)
Title:Resource-dependent complexity of quantum channels
Abstract, slides, video
Quantum complexity theory is concerned with the amount of elementary quantum resources needed to build a quantum system or a quantum operation. The fundamental question in quantum complexity is to define and quantify suitable complexity measures. In this talk, combining the approach introduced by Li-Bu-Koh-Jaffe-Lloyd and well-established tools from noncommutative geometry, we propose a unified framework for resource-dependent complexity measures of general quantum channels, also known as Lipschitz complexity. This framework is suitable to study the complexity of both open and closed quantum systems. The central class of examples in this paper is the so-called Wasserstein complexity. We use geometric methods to provide upper and lower bounds on this class of complexity measures. Finally, we study the Lipschitz complexity of random quantum circuits and dynamics of open quantum systems in finite dimensional setting. In particular, we show that generically the complexity grows linearly in time before the return time. This is the same qualitative behavior conjecture by Brown and Susskind . We also provide an infinite dimensional example where linear growth does not hold.
November 8, 2023. 14:30 (Beijing time)
Speaker: Renat Gumerov (Kazan University)
Title:Coverings of compact groups and automorphisms of semigroup C*-algebras
September 30, 2023. 14:30 (Beijing time)
Speaker: Yongle Jiang (Dalian University of Technology)
Title:On Determining G-invariant von Neumannn subalgebras in L(G)
Abstract, slides, video
Let G be a countable discrete group. In this talk, we are interested in the problem of completely determining G-invariant von Neumann subalgebras in L(G). If every G-invariant von Neumann subalgebra M in L(G) is of the form M=L(H) for some normal subgroup H of G, then we call this group G has the invariant von Neumann subalgebras rigidity (ISR) property. We discuss the problem of determining which group G has this ISR property and other related recent work on it. Part of this talk is based on joint work with Dr. Tattwamasi Amrutam.
September 13, 2023. 14:30 (Beijing time)
Speaker: Manish Kumar (IMPAN)
Title: Factoriality of q-Araki-Woods von Neumann algebras
Abstract, video
We discuss the factoriality, non-injectivity, and fullness question of q-Araki-Woods von Neumann algebras, constructed by Hiai. These algebras are non-tracial coun-terparts of q-Gaussian algebras, which combine the q-deformations of free group fac-tors due to Bozejko-Kummerer-Spiecher, and quasi-free deformations of Shlyakht-enko. We will discuss our approach using conjugate/dual variables in order to solve the mentioned problems. This is joint work with Adam Skalski and Mateusz Wasilewski.
August 30, 2023. 14:30 (Beijing time)
Speaker: Mingming Cao (Instituto de Ciencias Matemáticas)
Title: A compact extension of Journé’s T1 theorem on product spaces
Abstract,video
In the 1980s, David and Journé proved the original theorem, which gave a characterization of the boundedness for Calderón–Zygmund operators based on testing conditions. Soon after, using the vector-valued Calderón–Zygmund theory, Journé first established a bi-parameter theorem. However, the theorem to deduce compactness of multi-parameter singular integrals has been open in the last several years. The purpose of this talk is to develop a general theory of the compactness for a class of bi-parameter singular integrals.
June 21, 2023. 16:00 (Beijing time)
Speaker: Cheng Chen (Sun Yat-sen University)
Title: Semigroup C*-algebras arising from graphs of monoids
Abstract, slides, video
Semigroup C*-algebras provide abundant examples in C*-algebras. For semigroups that are far from groups, we encounter completely new phenomena which are not visible in the group case. In the talk, we will introduce a special class of C*-algebras, namely semigroup C*-algebras arising from graphs of monoids. We will analyse their structral properties, including closed invariant subsets and topological freeness of the groupoids as well as simplicity, nuclearity, pure infiniteness and K-theory of the semigroup C*-algebras. Finally, we will give a classification of boundary quotients of the semigroup C*-algebras.
June 14, 2023. 16:00 (Beijing time)
Speaker: Samya Kumar Ray (Indian Statistical Institute Kolkata)
Title: Isometric embeddability of S_m^q into S_n^p
Abstract,video
One of the most important questions in Banach space geometry is when does a Ba-nach space embed into another Banach space isometrically or almost isometrically.In this talk, we discuss some results regarding existence of isometric embeddings of S_m^q into S_n^p where S_n^p is the usual Schatten-p class over n × n complex matrices. We also present some results when p and q are also allowed to be less than l. We will explain several new ingredients related to perturbation theory of linear operators, namely Kato-Rellich theorem, theory of multiple operator integrals,norm-parallelism and Birkhoff-James orthogonality, followed by thorough and careful case by case analysis, which are essential to our work. This talk is based on work done in collaboration with Arup Chattopadhya, Guixiang Hong, Avijit Pal and Chandan Pradhan.
May 24, 2023. 16:00 (Beijing time)
Speaker: Sergei Akbarov (National Research University Higher School of Economics)
Title: Stereotype dualities in Geometry
Abstract, slides, video
The natural parallels between the four big geometric disciplines in mathematics,
- algebraic geometry,
- complex geometry,
- differential geometry,
- topology,
can be explained by the fact that these disciplines appear as a visual image when studying the very same reality with the help of different observation tools.
A construction that formalizes this idea is called an envelope. This is a special kind of functor in category theory, generated by a class of morphisms chosen as the observation tools. In the case of the mentioned geometric disciplines, the common reality they reflect is the theory of topological (more precisely, stereotype) algebras, and the functors that transform this reality into the last three disciplines are respectively
- the holomorphic envelope, where the observation tools are the homomorphisms into Banach algebras,
- the smooth envelope, where the observation tools are the so called differential homomorphisms into C*-algebras with the joined self-adjoint nilpotent elements, and
- the continuous envelope, where the observation tools are the homomorphisms into C*-algebras. Each of these functors generates, apart from the corresponding geometric discipline itself, a special kind of duality in it, which is called stereotype duality, and which generalizes the famous Pontryagin duality for locally compact Abelian groups (to some class of not necessarily commutative groups).
This leads to an intriguing picture, where it becomes possible to compare these geometries as disciplines, to find common features, differences, generalizations, new examples, and so on. In my talk I'm going to give accurate definitions and discuss some details of this picture.
May 7, 2023. 16:00 (Beijing time)
Speaker: Jianchao Wu (Fudan University)
Title: The Novikov conjecture, groups of diffeomorphisms, and Hilbert-Hadamard spaces
Abstract, slides, video
The Novikov conjecture is a prominant problem in differential topology. The operator K-theoretic approach provided by noncommutative geometry has yielded some of the best results that verify this conjecture for vast classes of groups. A natural class of groups for which the conjecture remains largely mysterious is that of countable groups of diffeomorphisms on smooth manifolds. In an upcoming joint paper with Sherry Gong, Zhizhang Xie, and Guoliang Yu, we prove that the (rational strong) Novikov conjecture holds for geometrically discrete countable subgroups of the group of diffeomorphisms of any closed smooth manifold. This removes the volume-preserving condition in a previous joint paper with S. Gong and G. Yu.
April 28, 2023. 10:00 (Beijing time)
Speaker: Dmitriy Zanin (University of New South Wales)
Title: Principal symbol mapping for Heisenberg groups and/or contact manifolds
Abstract, slides, video
In this talk, I will introduce the notion of principal symbol. Firstly, in the archaic context of pseudo-differential operators, then in the general C*-algebraic context. Examples to be provided are (a) rather old ones, such as Euclidean spaces and tori (and their non-commutative analogues) and (b) very new ones, such as stratified groups (in particular, Heisenberg groups). I will also demonstrate how does the principal symbol mapping behave under the natural action of diffeomorphisms (in the Euclidean case) and Heisenberg diffeomorphisms (in the Heisenberg group case). This is needed to extend the notion of the principal symbol to the manifolds (from Euclidean case) and to the contact manifolds (from the Heisenberg case). Corresponding globalization theorems will be provided. As an application, I will present the Connes Trace Theorem (including, in particular, the spectrally correct sub-Riemannian volume).
April 26, 2023. 16:00 (Beijing time)
Speaker: Xin Ma (University of Memphis)
Title: Soficity, Amenability, and LEF-ness for topological full groups
Abstract, video
Topological full groups, as an algebraic invariant, were introduced to study continuous orbit equivalence relations by Giordano, Putnam, and Skau. Then, these groups have been found applications to geometric group theory by providing interesting examples with certain properties such as simplicity, soficity, amenability, and LEF-ness. In this talk, we will show new methods of establishing the soficity and LEF-ness for topological full groups. Moreover, we will explain how can one obtain amenability from the sofic approximations when the acting group is amenable and the action is free and distal.
April 19, 2023. 16:00 (Beijing time)
Speaker: Martijn Caspers (Delft University of Technology)
Title: A Sobolev estimate for radial multipliers on SL(n,R)
Abstract, video
Lp-Fourier multipliers form a central tool in harmonic analysis on Euclidean spaces as well as the torus. In this talk we are concerned with natural generalisations of such multipliers on non-abelian groups and focus on the special case of SL(n,R). We show how to construct such Lp-Fourier multipliers by requiring sufficient smoothness of the symbols in the spirit of Hormander-Mikhlin and Calderon-Torchinsky. Our methods in particular give new results if p approximates 2. If time permits I will also report on versions of the De Leeuw restriction theorem for SL(n,R) and SL(n,Z). The latter is joint work with Bas Janssens, Amudhan Krishnaswamy-Usha and Lukas Miaskiwskyi.
March 22, 2023. 16:00 (Beijing time)
Speaker: Marat Pliev (Southern Institute of Mathematics of Russian Academy of Sciences)
Title: Orthogonally additive operators in vector lattices and around
Abstract, slides, video
In first part of the talk we discuss basic examples and properties of orthogonally additive operators in vector and Banach lattices emphasizing on connections with other areas of the modern mathematics. In the second part we present some open problems concerning order and topological properties of orthogonally additive operators in Banach and vector lattices.
March 15, 2023. 16:00 (Beijing time)
Speaker: Fedor Sukochev (University of New South Wales)
Title: Quantitative estimates for the functional calculus on the Schatten p-classes, 0<p<∞
March 8, 2023. 16:00 (Beijing time)
Speaker: Hongyin Zhao (University of New South Wales)
Title: Perturbation theory of commuting self-adjoint operators and related topics
Abstract, slides (part1, part2), video
This talk contains two parts. In the first part, we give an overview of perturbation theory of operators, including Weyl-von Neumann theorem and Kato-Rosenblum theorem, and introduce Voiculescu’s quasicentral modulus. In the second part, we introduce our recent results in the extension of Voiculescu’s results to the case of von Neumann algebras and factors.
December 7, 2022. 16:00 (Beijing time)
Speaker: Alexandros Eskenazis (Institut de mathématiques de Jussieu, CNRS)
Title: Learning low-degree functions on the discrete hypercube
Abstract, slides, video
Let f be an unknown function on the n-dimensional discrete hypercube. How many values of f do we need in order to approximately reconstruct the function? In this talk, we shall discuss the random query model for this fundamental problem from computational learning theory. We will explain a newly discovered connection with a family of polynomial inequalities going back to Littlewood (1930) which will in turn allow us to derive sharper estimates for the query complexity of this model, exponentially improving those which follow from the classical Low-Degree Algorithm of Linial, Mansour and Nisan (1989), while maintaining a running time of the same order. Time permitting, we will also show a matching information-theoretic lower bound. Based on joint works with Paata Ivanisvili (UC Irvine) and Lauritz Streck (Cambridge).
November 30, 2022. 16:00 (Beijing time)
Speaker: Léonard Cadilhac (Sorbonne University)
Title: Marcinkiewicz interpolation for non-commutative maximal norms
Abstract, slides (partly written by Eric Ricard), video
In a landmark paper published in 2007, M. Junge and Q. Xu made significant contributions to noncommutative ergodic theory and in particular furthered our understanding of non-commutative maximal norms. One of their key results is a Marcinkiewicz-type interpolation theorem for those norms, for which they provide a long and technical proof. I will present recent work in collaboration with E. Ricard, where we revisit this theorem, providing a more compact proof and improving on the statement. The talk will first discuss non-commutative maximal norms and briefly introduce interpolation, then detail the main ideas and result, and finally present its more technical variants as well as some of the challenges ahead.
November 23, 2022. 16:00 (Beijing time)
Speaker: Boris Kashin (Russian Academy of Sciences)
Title: On some applications and connections of Functional Analysis
Abstract, slides, video
In the last two decades, due to the rapid development of computer science, the results from functional analysis (including the geometry of convex bodies and approximation theory in normed spaces) are used rather extensively in practical applications. At the same time, the above mentioned branches of functional analysis and theoretical computer science are getting closer to each other, and methods from each of them turn out to be applicable in the other. In this talk, we will discuss a number of results that illustrate those trends.
November 16, 2022. 16:00 (Beijing time)
Speaker: Alexander Frei (University of Copenhagen)
Title: Operator algebras and quantum information:
1) Connes implies Tsirelson and 2) Robust self-testing (hot topic)
Abstract, slides, video
We give a simple proof of Connes implies Tsirelson, and further advertise a hot topic in quantum information: optimal states and robust self-testing. We showcase here how operator algebraic techniques can be quite fruitful.
For this we begin with by recalling quantum strategies in the context of non-local games, and their description in terms of the state space on the full group algebra of certain free groups. With this description at hand, we then directly obtain the main result via an elementary lifting result by Kim, Paulsen and Schafhauser:
The Connes embedding problem implies the synchronous Tsirelson conjecture.
As such the entire proof is elementary, and bypasses all versions of Kirchberg's QWEP conjecture and thelike, as well as any reformulation such as in terms of the micro state conjecture. Moreover, it should be (likely) easier to construct minimal nonlocal games as counterexamples for the synchronous Tsirelson conjecture (which is equivalent to the full Tsirelson conjecture but in a non-trivial way) and so also nonamenable traces for above groups, in other words non-Connes embeddable operator algebras.
After this we continue (as much as time permits) with an advertisement for a topic in quantum information (a hot one):
Device-independent certification of quantum states – more precisely ROBUST SELF-TESTING –
which has tremendous importance for the coming era of practical quantum computingand we showcase how operator algebraic techniques can be quite fruitful here.More precisely, we illustrate these techniques on the following two prominent classes of nonlocal games:
1) The tilted CHSH game.
We showcase here how to compute the quantum value using operator algebraic techniques, and how to use the same to derive uniqueness for entire optimal states, including all higher moments as opposed to correlations defined on two-moments only, where the latter compares to traditional self-testing.Moreover, we report in this example on previously unknown phase transitions on the uniqueness of optimal states when varying the parameters for the tilted CHSH game.
2) The Mermin–Peres magic square and magic pentagram game. As before, we also note here uniqueness of optimal states, which in these two examples is a basically familiar result.
The first part is based on preprint: https://arxiv.org/abs/2209.07940
The second part on self-testing (and further robust self-testing) is based on https://arxiv.org/abs/2210.03716 and upcoming joint work with Azin Shahiri.
October 19, 2022. 16:00 (Beijing time)
Speaker: Piotr Nayar (University of Warsaw)
Title: The Khintchine inequality
Abstract, slides, video
We shall discuss the celebrated moment comparison for weighted sums of i.i.d. symmetric Bernoulli random variables, proved in 1923 by Khinchine. This inequality influenced several areas of mathematics, including probability theory, Banach spaces theory and convex geometry. We will focus on the problem of finding optimal constants and present the most elegant proofs, both old and new.
October 13, 2022. 20:30 (Beijing time)
Speaker: Jingyin Huang (Ohio State University)
Title: Measure equivalence superrigidity for some generalized Higman groups
Abstract, slides, video
In the 1950s, Higman introduced the first class of examples of infinite finitely presented groups without any non-trivial finite quotient. We study Higman groups from the viewpoint of measure equivalence - a notion introduced by Gromov as a measurable counterpart to quasi-isometry. For most Higman groups and some generalizations, we prove a strong measure equivalence rigidity theorem. In this talk, I'll sketch the proof, discuss some of the consequences, and compare to some other measure equivalence rigidity/flexibility results in the literature. This is joint work with Camille Horbez.
September 28, 2022. 13:30 (Beijing time)
Speaker: Benoît Collins (Kyoto University)
Title: Properties of random tensor matrices with some applications to Quantum Information Theory
Abstract, video
We will describe a research project in collaboration with Luca Lionni and Razvan Gurau where we study the joint behavior of iid random elements in tensors of matrix algebras whose law is invariant under local conjugations. We will also mention some results on the norm of tensors of random matrices and explain some applications to QIT.
September 21, 2022. 16:00 (Beijing time)
Speaker: Christian Voigt (University of Glasgow)
Title: Infinite quantum permutations
Abstract, slides, video
In this talk I will discuss an approach to study quantum symmetries of infinite sets and graphs. This leads to discrete quantum groups, in analogy to the quantum symmetry groups of Wang and Banica/Bichon. For finite sets and graphs, the resulting quantum groups can in fact be viewed as discretisations of the former (compact) quantum groups. I will discuss a number of examples, and highlight some intriguing open problems as well.
August 31, 2022. 16:00 (Beijing time)
Speaker: Vladimir Al. Osipov (Holon Institute of Technology)
Title: Integrability in random matrix theory and its applications
Abstract, slides, video
Random matrices are widely used to model quantum systems with chaos and disorder. In such models, the observable is expressed as a quantum operator averaged over an ensemble of random matrices with a given probability measure. In my talk, I demonstrate a general approach, “the random matrix integrable theory”, to the nonperturbative calculation of the random-matrix integrals. With this approach, the internal symmetries of the integration measure, expressed in terms of highly non-trivial nonlinear relations for the original integral (the Toda lattice hierarchy, the Kadomtsev-Petviashvili hierarchy) and the relations following from the deformation of the integration measure (Virasoro constraints), are used to represent the integral as a solution of differential equations, where the differentials are taken over the internal (physical) parameters of the model [1,2]. This method represents a particular implementation of results obtained within a more general theory of $\tau$-functions. In particular, the central theorem of this theory states the existence of the Toda lattice and Kadomtsev-Petviashvili hierarchies for the typical random-matrix integrals.
The particular implementation of the integrable theory will be discussed in the example of the physical problem of quantum transport in chaotic cavities [3,4]. A brief introduction to the physics of the problem and the advantage of the integrable theory method for calculation of the conductance cumulants, and of the shot-noise-conductance joint cumulants are going to be presented. In particular, we demonstrate how the conductance cumulant generation function can be expressed in terms of the solution of the Painleve V transcendent equation. In addition, the results of the integrable theory implementation to the averaged random-matrix characteristic polynomials [1], and also for the problem of the power spectrum of the eigenlevel sequences in the quantum chaotic system [2,5] will be discussed.
[1] V.Al.Osipov, E.Kanzieper, “Correlations of RMT characteristic polynomials and integrability: Random Hermitian matrices”, Annals of Physics325 (2010) 2251
[2] R.Riser, V.Al.Osipov, E.Kanzieper, “Nonperturbative theory of power spectrum in complex systems”, Annals of Physics413 (2020) 168065
[3] V.Al.Osipov, E.Kanzieper, “Integrable theory of quantum transport in chaotic cavities”, Phys.Rev.Let.101 (2008) 176804
[4] V.Al.Osipov, E.Kanzieper, “Statistics of thermal to shot noise crossover in chaotic cavities”, J.Phys.A:Math.Theor.42 (2009) 475101
[5] R.Riser, V.Al.Osipov, E.Kanzieper, “Power-spectrum of long eigenlevel sequences in quantum chaology”, Phys.Rev.Let.118 (2017) 204101
July 6, 2022. 16:00 (Beijing time)
Speaker: Vladimir Manuilov (Moscow State University)
Title: On Hochshild cohomology of uniform Roe algebras with coefficients in uniform Roe bimodules
Abstract, slides, video
Uniform Roe algebras play an important role in noncommutative geometry. It was shown recently by M. Lorentz and R. Willett that all bounded derivations of the uniform Roe algebras of metric spaces of bounded geometry are inner. Here we calculate the space of outer derivations of the uniform Roe algebras with coefficients in uniform Roe bimodules related to various metrics on the two copies of the given space. We also give some results on the higher Hochschild cohomology with coefficients in uniform Roe bimodules.
June 22, 2022. 19:30 (Beijing time)
Speaker: Ping Zhong (University of Wyoming)
Title: The Brown measure of the sum of a free random variable and an elliptic deformation of Voiculescu's circular element
Abstract, slides, video
The circular element is the most important example of non-normal random variable used in free probability, and its Brown measure is the uniform measure in the unit disk. The circular element has connection to asymptotics of non-normal random matrices with i.i.d. entries. We obtain a formula for the Brown measure of the addition of an arbitrary free random variable
and circular element c, which is known to be the limit empirical spectral distribution of deformed i.i.d. random matrices.
Generalizing the case of circular and semi-circular elements, we also consider , a family of elliptic deformations of
, that is
-free from
. Possible degeneracy then prevents a direct calculation of the Brown measure of
. We instead show that the whole family of Brown measures of operators
are the push-forward measures of the Brown measure of
under a family of self-maps of the complex plane, which could possibly be singular. The main results offer potential applications to various deformed random matrix models. This work generalizes earlier results of Bordenave-Caputo-Chafai, Hall-Ho, and a joint work with Ho.
June 15, 2022. 19:30 (Beijing time)
Speaker: Jorge Castillejos (National Autonomous University of Mexico)
Title: The Toms-Winter regularity conjecture
Abstract, slides, video
The classification programme of simple nuclear C*-algebras asserts one can classify such C*-algebras in terms of an inviariant constructed out of K-theory and tracial information. However, in order to be able to use these classifications results, one must verify a topological type regularity property first. The Toms-Winter conjecture predicts that this regularity condition is equivalent to other type of regularity properties which might be easier to verify. In this talk, I will present an overview of this conjecture.
June 8, 2022. 19:30 (Beijing time)
Speaker: Roland Speicher (Saarland University)
Title: A dual and a conjugate system for q-Gaussians for all q
Abstract, slides, video
q-Gaussian random variables, for some fixed real with , are of the form
, where the
are operators satisfying the q-relations
. Understanding the properties of the non-commutative distributions of those deformations of classical multivariate Gaussian distributions as well as their associated operator algebras -- in particular, whether and how they depend on q -- has been of central interest in the last 30 years. I will give an introduction and survey on those q-relations and in particular report also some recent progress (from joint work with A. Miyagawa) on the existence of dual systems and conjugate systems for the q-Gaussians. Special focus is on the fact that those results are for the whole interval (-1,+1), and not just for some restricted set of q.
June 1, 2022. 16:00 (Beijing time). Mingde Building, B201-1
Speaker: Fedor Sukochev (University of New South Wales)
Title: Quantum differentiation and integration for the quantum plane
Abstract, slides, video
We explain recent results concerning (quantum) differentials and integrals on the noncommutative (Moyal) plane. We give full characterisation of elements on the noncommutative (Moyal) plane such that their quantum derivatives belong to the weak Schatten class , which means that these derivatives are d-times integrable in the quantum integration sense. We then calculate the quantum integration of these derivatives by adapting Connes' integration formulae to the noncommutative (Moyal) plane. This is a joint work with E. McDonald and X. Xiong.
May 25, 2022. 16:00 (Beijing time). Mingde Building, B201-1
Speaker: Ke Li (Harbin Institute of Technology)
Title: Reliability Function of Quantum Information Decoupling
Abstract
Quantum information decoupling is a fundamental information processing task, which also serves as a crucial tool in a diversity of topics in quantum physics. I will talk about our recent results on its reliability function, that is, the best exponential rate under which perfect decoupling is asymptotically approached. We have obtained the exact formula when the decoupling cost is below a critical value. In the situation of high cost, we provide upper and lower bounds. These results are given in terms of the sandwiched R\'enyi divergence, providing it with a new type of operational meaning. (Based on joint work with Yongsheng Yao, arXiv:2111.06343)
May 18, 2022. 16:00 (Beijing time)
Speaker: Ignacio Vergara (Leonhard Euler International Mathematical Institute in Saint Petersburg)
Title: Around Cowling's conjecture
Abstract, slides, video
Two very important concepts arose from Haagerup's highly influential work on the reduced C*-algebra of the free group: weak amenability and the Haagerup property. It is an open problem to determine whether weak amenability with Cowling-Haagerup constant 1 implies the Haagerup property. This is often referred to as Cowling's conjecture. In this talk, I will give an overview of this question, and I will discuss a recent progress in this direction: Every countable weakly amenable group with Cowling-Haagerup constant 1 admits a proper cocycle for a uniformly bounded representation on a subspace of an L1 space.
May 11, 2022. 16:00 (Beijing time)
Speaker: Mateusz Wasilewski (IMPAN Warsaw)
Title: On the isomorphism class of q-Gaussian C*-algebras for infinite variables
Abstract, slides, video
Bożejko and Speicher introduced q-Gaussian variables to produce examples of generalized Brownian motions. The resulting von Neumann algebras -- the q-Gaussian algebras -- can be viewed as deformations of the free group factors. It is a very natural question whether these von Neumann algebras are actually isomorphic to the free group factors. Guionnet and Shlyakhtenko introduced the free monotone transport techniques and provided a partial answer: if the number of variables is finite and the parameter q is very small then we do get an isomorphism. There are no results known for infinitely many variables and in my talk I plan to describe a related result about q-Gaussian C*-algebras -- in the infinite case they are not isomorphic to their free counterparts. The von Neumann algebraic case remains open.
Joint work with Matthijs Borst, Martijn Caspers and Mario Klisse.
May 4, 2022. 16:00 (Beijing time)
Speaker: Joseph Lehec (Université Paris Dauphine)
Title: The Kannan-Lovász-Simonovits conjecture up to polylog
Abstract, slides, video
The Kannan-Lovász-Simonovits conjecture asserts that high dimensional log-concave probability measures satisfy a certain universal concentration property. In a recent joint work with Bo’az Klartag we prove that this conjecture holds true up to a factor that is polylogarithmic in the dimension. In this talk I’ll mostly speak about the context around this conjecture, in particular I’ll present some of its numerous consequences. If time abides I’ll say a few words about our proof towards the end of the talk.
April 20, 2022. 16:00 (Beijing time)
Speaker: Cyril Houdayer (University of Paris-Saclay)
Title: Noncommutative ergodic theory of lattices in higher rank simple algebraic groups
Abstract, slides
In this talk, I will present a noncommutative Nevo-Zimmer theorem for actions of lattices in higher rank simple algebraic groups on von Neumann algebras. This extends to the realm of algebraic groups defined over arbitrary local fields the noncommutative Nevo-Zimmer theorem we obtained with Rémi Boutonnet in 2019 for real Lie groups.
I will discuss various applications of the above theorem to topological dynamics, unitary representations and operator algebras. I will also present a noncommutative analogue of Margulis’ factor theorem and discuss its relevance regarding Connes’ rigidity conjecture for group von Neumann algebras of higher rank lattices.
This is based on joint work with Uri Bader and Rémi Boutonnet (arXiv:2112.01337)




