题目：The Brown measure of the sum of a free random variable and an elliptic deformation of Voiculescu's circular element
报告人：Ping Zhong (怀俄明大学)
时间：2022年6月22日（星期三），19:30-21:00
地点：哈工大明德楼B区201报告厅
Zoom会议：会议号：824 7045 6491，会议密码：123399，链接：
https://zoom.us/j/82470456491?pwd=dGswU3d3RGd1L1d4a3ZvSXdnakVkUT09
摘要：The circular element is the most important example of non-normal random variable used in free probability, and its Brown measure is the uniform measure in the unit disk. The circular element has connection to asymptotics of non-normal random matrices with i.i.d. entries. We obtain a formula for the Brown measure of the addition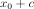 
of an arbitrary free random variable 
and circular element c, which is known to be the limit empirical spectral distribution of deformed i.i.d. random matrices.
Generalizing the case of circular and semi-circular elements, we also consider 
, a family of elliptic deformations of 
, that is 
-free from 
. Possible degeneracy then prevents a direct calculation of the Brown measure of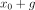 
. We instead show that the whole family of Brown measures of operators 
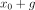are the push-forward measures of the Brown measure of 
under a family of self-maps of the complex plane, which could possibly be singular. The main results offer potential applications to various deformed random matrix models. This work generalizes earlier results of Bordenave-Caputo-Chafai, Hall-Ho, and a joint work with Ho.
更多相关信息请参见泛函分析研讨班网页。
