Casey's theorem in hyperbolic geometry

发布时间：2024-04-11浏览次数：10

题目：Casey's theorem in hyperbolic geometry

报告人：Nikolay Abrosimov (索伯列夫数学研究所，新西伯利亚)

时间：2024年4月15日（星期一），14:30-15:30

地点：明德楼B201-1

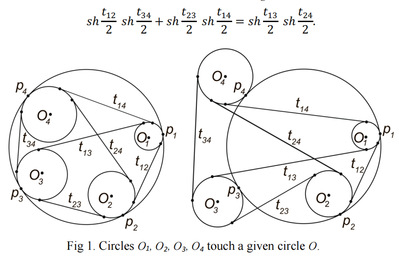
摘要：In 1881 Irish mathematician John Casey generalized Ptolemy’s theorem in the following way (see [1], p. 103). Casey’s theorem. Let circles O1, O2, O3, O4 on a plane touch given circle O in vertices p1, p2, p3, p4 of a convex quadrilateral. Denote by tij the length of a common tangent of the circles Oi and Oj. If O separates Oi and Oj then the internal tangent should be taken as tij else the external tangent should be taken. In both cases we assume that the tangents are exist. Then

In our paper [2], we produce hyperbolic version of Casey’s theorem.

Theorem 1. Let circles O1, O2, O3, O4 on the hyperbolic plane H2 touch given circle O in vertices p1, p2, p3, p4 of a convex quadrilateral. Denote by tij the length of a common tangent of the circles Oi and Oj. If O separates Oi and Oj then the internal tangent should be taken as tij else the external tangent should be taken. In both cases we assume that the tangents are exist. Then

References:

[1] J. Casey, A sequel to the first six books of the Elements of Euclid, containing an easy introduction to modern geometry, with numerous examples, 5th. ed., Hodges, Figgis and Co., Dublin 1888.

[2] N.V. Abrosimov, L.A. Mikaiylova, Casey’s theorem in hyperbolic geometry // Siberian Electronic Mathematical Reports, 12 (2015), 354-360. DOI: https://doi.org/10.17377/semi.2015.12.029