Title: Optimal distribution estimates for commutators and Marcinkiewicz multipliers
Speaker: Fedor Sukochev
Time: Wednesday, October 22, 2025, 16:00-17:00 (UTC+8)
Venue: Gewu Building, Room 315
Zoom ID: 932 9695 9808 (Password: 856375)
Link: https://zoom.us/j/93296959808?pwd=LKqmrFebv5dhEHzFbRcMBGiWKALRIe.1
Abstract: The main objective of this talk is to discuss the distributional estimates for (i) commutators with Calderón-Zygmund integral operators; (ii) Marcinkiewicz multipliers; (iii) Littlewood-Paley square function, via semigroup {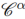 
}α>0 generated by Cesàro operator. In each of the cases (i)-(iii) we obtain new estimates of the distribution of elements in the range of the underlying operators in terms of the distribution function of the input function. Our method allows us to obtain optimal estimates shedding additional light at the results due to Pérez (1995), Tao and Wright/Bakas et al. (2001/2024), Bourgain (1989). The main feature of the distributional form inequalities lies in its broad applicability across diverse problems in analysis, e.g. they allow obtaining estimates in wide range of symmetric quasi-Banach interpolation spaces between Lp and Lq(1 < p < q < ∞), not just for Lp-spaces (1 < p < ∞). This is a joint work with Fulin Yang, Dmitriy Zanin and Dejian Zhou accepted for publication in Math. Annalen.
