Systoles and Coxeter groups

题目：Systoles and Coxeter groups

报告人：Olivier Mathieu(法国科学研究中心，里昂)

时间：5月6日（星期一），15:30-16:30

地点：明德楼B201-1报告厅

摘要：Given a closed hyperbolic surface, a systole is a closed geodesic of shortest length. A generic surface of genus  has a unique systole which cuts it into one or two noncontractible pieces. However, there are closed hyperbolic surfaces of genus 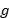, whose set of systoles fills the surface, i.e. it cuts the surface into polygons. In general, it is easy to find surfaces with a large number of systoles which fill. A classical example is the Bolsa surface of genus 2 with 12 systoles. Here we are interested to find surfaces for which the set of systoles is filling while being small. In fact, our approach provides surfaces with significatively less systoles than the previously known examples. Then we will briefly outline a consequence in Teichmüller theory. Our construction is based on the theory of Coxeter groups, especially the arithmetic properties of the Tits representation. From a geometric viewpoint, it involves hyperbolic tessellations. Although this work mixes hyperbolic geometry and representation theory, our presentation will be quite elementary.

报告人简介：

更多相关信息请参见 杰出学者讲座