题目:Topological entropy for non-archimedean dynamics
报告人:谢俊逸(北京大学)
时间:2022年12月8日(星期四),14:00-15:15
地点:Zoom会议,会议号:898 2596 2251,密码:2022
摘要:The talk is based on a joint work with Charles Favre and Tuyen Trung Truong. We prove that the topological entropy of any dominant rational self-map of a projective variety defined over a complete non-Archimedean field is bounded from above by the maximum of its dynamical degrees, thereby extending a theorem of Gromov and Dinh-Sibony from the complex to the non-Archimedean setting. We proceed by proving that any regular self-map which admits a regular extension to a projective model defined over the valuation ring has necessarily zero entropy. To this end we introduce the 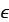 -reduction of a Berkovich analytic space, a notion of independent interest.
-reduction of a Berkovich analytic space, a notion of independent interest.
更多相关信息请参见Colloquium Talks

