Title: Deformation quantization of the Loday-Quillen-Tsygan
Speaker: Farkhod Eshmatov（New Uzbekistan University）
Time: 12.23 (Tuesday), 10:00-11:00
Venue: Mingde Building B201-1
Abstract:The Loday/Quillen-Tsygan theorem identifies the graded symmetric algebra on the cyclic homology of an associative algebra A with the Lie algebra homology of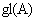 
. In this talk, I will describe a deformation and quantization of this result.For a Koszul Calabi-Yau algebra A, we show that the primitive part of 
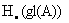carries a natural Lie bialgebra structure induced by the Poincarè duality of A, yielding a co-Poisson deformation of 
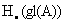. We further construct a Hopf algebra that quantizes this structure and lifts the Loday-Quillen-Tsygan isomorphism to the quantum level.This can be viewed as a quantization of the tangent map from the tangent complex of BGL to that of algebraic K-theory. (Joint work with X. Chen and M. Huang)
