一、 论坛日期：2025年7月13日（星期日）
二、 论坛时间：9:00-12:00
三、 论坛地点：格物楼315
Zoom会议号：918 6733 4150 密码：0713
四、 论坛安排
Ø 09:00-09:10 开幕式致辞
Ø 09:10-09:55 学术报告（线上）
题 目：Entropy meets geometry: Information-theoretic perspectives on geometric problems
报告人：李冬彬（阿尔伯塔大学）
Ø 09:55-10:40 学术报告（线上）
题 目：Monotone Perfection
报告人：徐韩萍(新加坡国立大学)
Ø 10:40-11:10 交流讨论
Ø 11:10-11:55 学术报告
题 目：(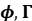
) and (
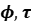)-module approaches to Galois Cohomology and related invariants
报告人：赵路明（北京大学）
Ø 11:55-12:00 闭幕式致辞
报告题目与摘要
Entropy meets geometry: Information-theoretic perspectives on geometric problems
李冬彬
阿尔伯塔大学
摘要: In this talk, we introduce new information-theoretic perspectives on two classical conjectures in convex and discrete geometry. The first is the Kneser– Poulsen conjecture, which asserts that the volume of a union of balls cannot increase when their centers are moved pairwise closer. The second, known as the dimensional Brunn–Minkowski conjecture, predicts that log-concave measures exhibit volume-like concavity when restricted to symmetric convex bodies. We approach these problems by formulating more general entropy based questions, whose resolution would imply both conjectures. In each case, we provide a complete solution in the setting of the Gaussian measure.
Monotone Perfection
徐韩萍
新加坡国立大学
摘要：This paper proposes a new equilibrium concept called “perfect monotone equilibrium” in Bayesian games, which strengthens the standard notion of monotone equilibrium by accounting for the possibility that players might choose unintended strategies due to a trembling hand. A perfect monotone equilibrium satisfies the important property of admissibility in Bayesian games with finitely many actions, and the property of limit undominatedness in settings with infinitely many actions. In a general class of Bayesian games where each player's action set is a sublattice of multi-dimensional Euclidean space and players' types are also multi-dimensional, a perfect monotone equilibrium is shown to exist under the supermodularity and increasing differences conditions. These conditions model the scenarios in which, informally, players' payoffs exhibit complementarity in their own actions and monotone incremental returns in their own types. To illustrate practical relevance, we extend the analysis to Bayesian games with discontinuous payoffs, including application such as first-price auctions, all-pay auctions, and Bertrand competitions. Our result further generalizes to the setting with more general action spaces and type spaces.
(
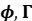) and (
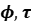)-module approaches to Galois Cohomology and related invariants
赵路明
北京大学
摘要：We begin by reviewing how the classical semi-linear algebra objects of p-adic Hodge theory—the various (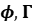
)-modules—compute the Galois and Iwasawa cohomology of p-adic representations. Building on the ideas of Breuil and Kisin, we then highlight the rapidly developing theory of (
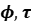)-modules, whose importance has been underscored by recent work of Scholze and collaborators on integral p-adic Hodge theory. Finally, we present our results that compute Galois cohomology via (
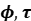)-modules in various settings and, time permitting, sketch parallel progress on the computation of Bloch-Kato Selmer groups using a Prismatic approach.
