Title: Non-commutative Neveu decomposition and associated ergodic theorems
Speaker: Diptesh Saha(Indian Statistical Institute, Delhi)
Time: Monday, May 13, 2024, 15:00-16:00
Location: Zoom Meeting ID: 439 550 2599; Passcode: 0513
Abstract: In ergodic theory, depending on the sense of convergence, there are mainly three different kinds of ergodic theorems, namely mean ergodic theorems (convergence in norm), pointwise ergodic theorems (a.e. convergence), and stochastic ergodic theorems (convergence in measure). To study Krengel’s stochastic ergodic theorem for a (not necessarily measure preserving) dynamical system, Neveu decomposition is an essential tool.
In this talk we will discuss some of this theorems in the non-commutative setting. We will begin with non-commutative Neveu decomposition. Then we will briefly discuss pointwise ergodic theorems in non-commutative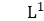 -spaces associated to the dynamical system
-spaces associated to the dynamical system , where
, where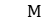 is a von Neumann algebra,
is a von Neumann algebra, 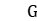 is either a group of polynomial growth, or
is either a group of polynomial growth, or 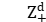 , or
, or 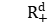 , or a finitely generated free group, and α denotes the action of
, or a finitely generated free group, and α denotes the action of 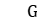 on
on 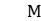 .
.
Finally, we combine the Neveu decomposition and the pointwise ergodic theorems discussed above to show a stochastic ergodic theorem. This is a joint work with Dr. Panchugopal Bikram.

