ANALYSIS SEMINAR
Title: Kuroda’s theorem for n-tuples in semifinite von Neumann algebras
Speaker: Hongyin Zhao (University of New South Wales)
Time: Wednesday, April 17, 2024, 16:00-17:30
Location: B201-1, Mingde Building
Zoom ID: 946 1307 0421, Password: 371188
Abstract: Kuroda’s Theorem is one of the fundamental results in perturbation theory. It states that, if J is a Banach ideal in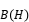 
that is not contained in the trace class, then for every self-adjoint operator b on H and every 
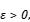there exists a diagonal operator d on H such that ∥b − d∥J < ε. In this talk, we will talk about an extension of Kuroda’s theorem for n-tuples of commuting self-adjoint operators affiliated with a semifinite von Neumann algebra 
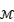, with respect to symmetric spaces associated with 
More information about the Analysis Seminar can be found here.
