Casey's theorem in hyperbolic geometry

Release time：2024-04-11Views：10

Title:Casey's theorem in hyperbolic geometry

Speaker:Nikolay Abrosimov（Sobolev Institute of Mathematics, Novosibirsk）

Time:Monday, April 15, 2024, 14:30-15:30

Location：Mingde Building B201-1

Abstract：In 1881 Irish mathematician John Casey generalized Ptolemy’s theorem in the following way (see [1], p. 103). Casey’s theorem. Let circles O1, O2, O3, O4 on a plane touch given circle O in vertices p1, p2, p3, p4 of a convex quadrilateral. Denote by tij the length of a common tangent of the circles Oi and Oj. If O separates Oi and Oj then the internal tangent should be taken as tij else the external tangent should be taken. In both cases we assume that the tangents are exist. Then

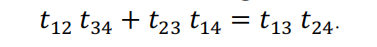
In our paper [2], we produce hyperbolic version of Casey’s theorem.

Theorem 1. Let circles O1, O2, O3, O4 on the hyperbolic plane H2 touch given circle O in vertices p1, p2, p3, p4 of a convex quadrilateral. Denote by tij the length of a common tangent of the circles Oi and Oj. If O separates Oi and Oj then the internal tangent should be taken as tij else the external tangent should be taken. In both cases we assume that the tangents are exist. Then

References:

[1] J. Casey, A sequel to the first six books of the Elements of Euclid, containing an easy introduction to modern geometry, with numerous examples, 5th. ed., Hodges, Figgis and Co., Dublin 1888.

[2] N.V. Abrosimov, L.A. Mikaiylova, Casey’s theorem in hyperbolic geometry // Siberian Electronic Mathematical Reports, 12 (2015), 354-360. DOI: https://doi.org/10.17377/semi.2015.12.029