Title:Playing with Kempner-like harmonic series
Speaker: Jean-Paul Allouche(CNRS, IMJ-PRG)
Time:Tuesday, May 30, 16:00-17:00
Location:Zoom Meeting, Meeting ID:832 6498 6834, password:2023
Abstract:Though the series of the inverses of integers diverges, a nice,now classical, result of Kempner (in 1914) states that the sum of the inverses of the integers whose expansion in base 10 contains no occurrence of a given digit converges. Several generalizations or extensions of this result have been given. In particular a paper of Farhi (in 2008) proves the somehow unexpected result that
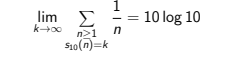
where s10(n) is the sum of the digits of n in base 10.
We show how to extend this result, first by replacing s10(n) with s2(n), the sum of the binary digits of the integer n; then by replacing s2(n) by any binary pattern counting sequence (i.e., any sequence aw(n) that counts the number of occurrences of a fixed block w of 0’s and 1’s in the binary expansion of the integer n).
More information about Colloquium Talks can be found here.

